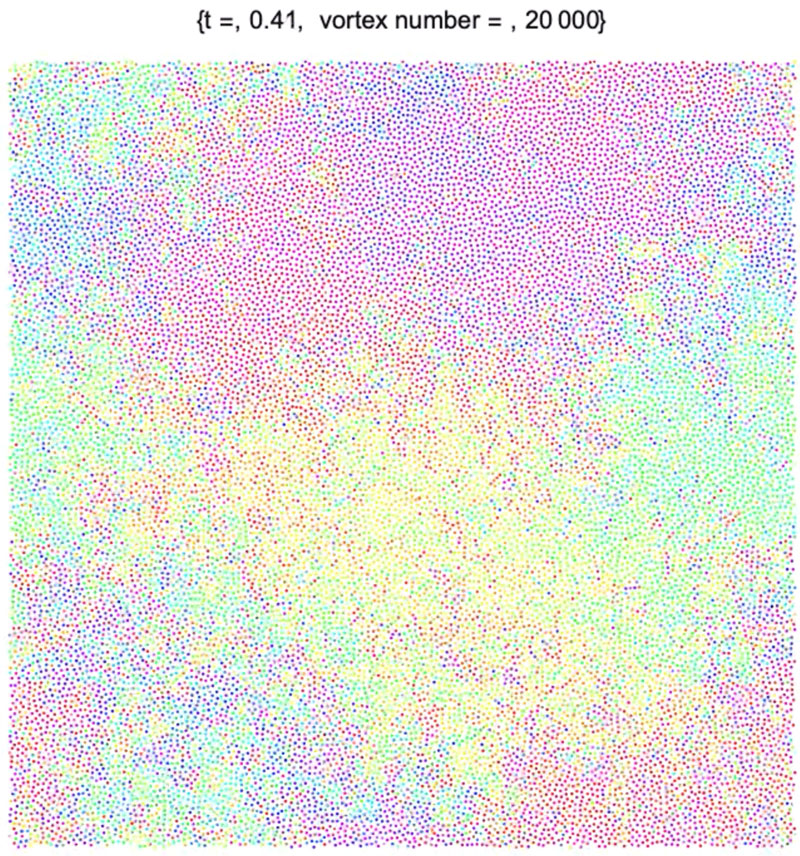PC1-4
Simulation of Collective Motion of Vortices Using Molecular + Field Dynamics Method
Nov. 29 10:45-11:00
*Jun Yamanaka1, Masaru Kato2
Department of Physics and Electronics, Osaka Prefecture University1
Department of Physics and Electronics, Osaka Metropolitan University2
In a type II superconductor under an external magnetic field, quantized vortices appear. Controlling vortices is important for application of superconductors. Especially, pinning and dynamics of vortices in a dirty superconductor have been studied widely.
Uchiyama et al investigated collective motion of vortices in a type II superconductor using the scanning tunneling microscope[1]. They found that vortex lattice are divided into vortex bundle separated by the glade plane of edge dislocation. In order to investigate origins of this collective motion of vortices, we simulate vortex dynamics in a moderately dirty superconductor using the molecular dynamics method (MD).
The MD is a computer simulation method for many particle dynamics, in which we solve equations of motion of particles numerically. In order to apply this method to the vortex dynamics, we treat vortices as particles in two dimensional space. The equation of motion for i-th vortex is given as,
η(dri)/dt=fdi +fpi +fvi +ffi
where is fCi is force by the current field. Pinning force fpi is given as,
fpi=-∇Vimp (r) |(r=ri )
and thermal fluctuation force ffi is given as,
〈ffi(t1)∙ffj(t2)〉=2ηkBTδijδ(t1-t2).
The Lorentz force fCi from the current field is derived from the overall total current J consisting of vortex currents and the external current is given as,
fCi=(1/c)J(ri )×Φ0z.
We consider 50 λ0 ×50 λ0 a square superconducting plate. In order to obtain the impurity potential and the current field, we use the finite element method (FEM). In the FEM, we divide the superconducting plate into random triangular elements. The maximum value of the impurity potential is Vimpmax. We show simulation results of the dynamics of the 20000 vortices as shown in Figure.
[1]K. Uchiyama, S. Suzuki, A. Kuwahara, K. Yamasaki, S. Kaneko, H. Takeya, K. Hirata, N. Nishida; Physica
C, 470 (2010) S795.
Keywords: Molecular Dynamics Method, Vortex Dynamics, Collective Motion, Vortex Pinning