PC1-6
Vortex states under in a superconductor under a helical magnetic field
Nov. 29 11:15-11:30
*Masaru Kato1
Osaka Metropolitan University, Japan1
Under an external field in a superconductor, there appear vortices. In a usual situation, the magnetic field is aligned in a single direction. So, all of vortices are parallel to the magnetic field. However, if the magnetic field is rotated, e.g. a double layer structure with a superconductor and a helical magnet, vortices might be rotated. When several vortices appear, these vortices interact with each other. The interaction between parallel vortices has been studied well. But the interaction between rotated vortices has not been studied well until now.
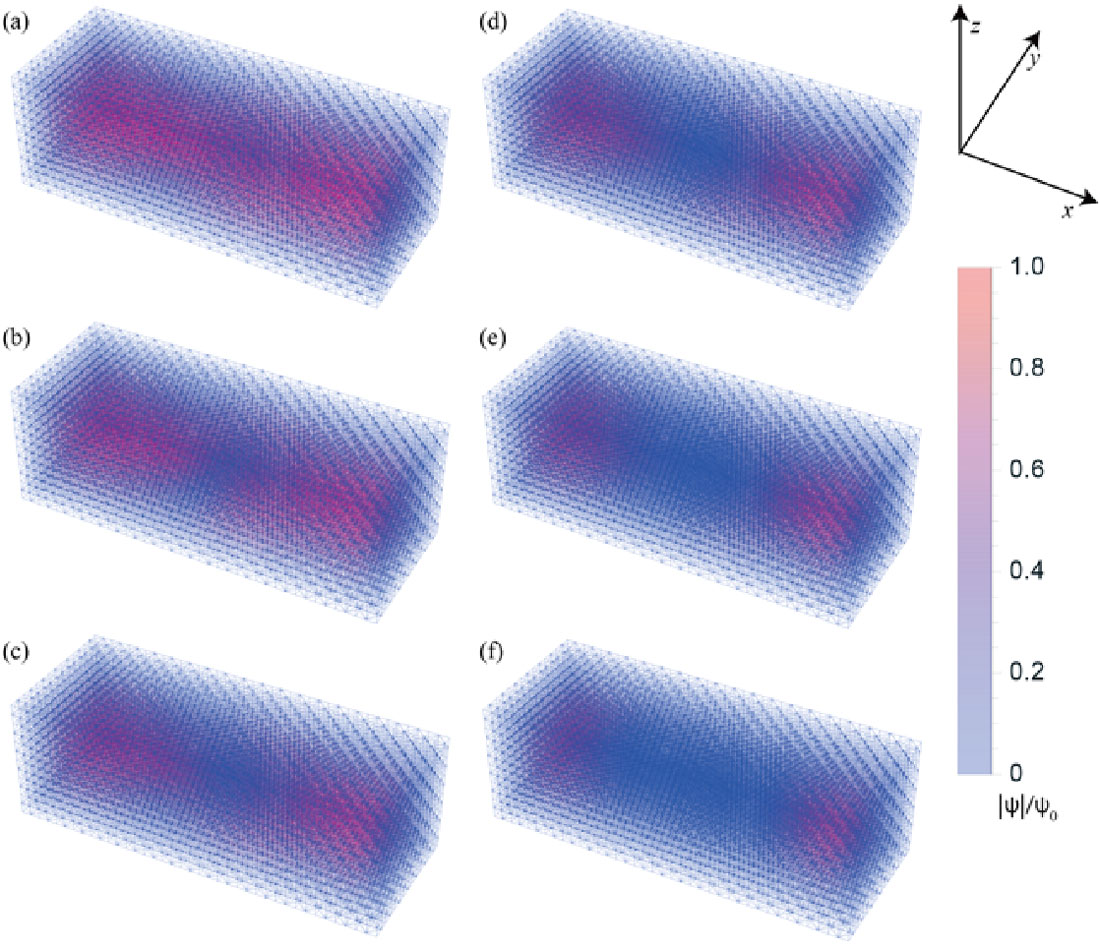
Previously, we studied vortex structure in a superconductor under a helical magnetic field. Solving the 3-dimensional Ginzburg-Landau (GL) equations with the 3-dimensional finite element method (3d-FEM), we obtained unusual magnetic structure (Fig.1) [1-3]. In Fig. 1, directions of two vortices are not parallel to those of the magnetic field.
In order to investigate vortex structures in detail, we consider several helical magnetic fields and solve the 3-d GL equations with the FEM. We find that superconducting transition temperature depends on the rotation pitch of the helical magnetic field. Also, vortex-vortex interaction depends on an angle between vortices. Sometime, they form an entangled structure. Moreover, cutting and reconnection of vortices occur. We will investigate the origin of these unusual vortex behaviors.
Figure.1 vortex structures under a helical magnetic field.
[1] S. Fukui, M. Kato, Y. Togawa, Supercond. Sci. Technol. 29 (2016) 125008.
[1] S. Fukui, M. Kato, Y. Togawa, O. Sato, J. Phys. Soc. Jpn. 87 (2018) 084701.
[2] S. Fukui, M. Kato, Y. Togawa, O. Sato, Physica C 589 (2021) 1353918.
Keywords: Vortex, Helical magnetic field, GInzburg-Landau equations, Finite Element Method